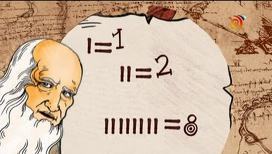
Дар замонҳои қадим нисбати ду ададро адад ҳисоб намекардаанд. Аввалин бор дар корҳои олимони мо - Мусо ал- Хоразмӣ (солҳои 787-850), Умари Хайём (1048-1131) ва Насируддини Тусӣ (1201-1274) ба маънии адад истифода шудани нисбат мушоҳида мешавад. Барои мисол ду масъалаҳои зерини Мусо ал-Хоразмиро моеварем:
- «Ду ададеро ёбед, ки суммаашон ба 10 ва нисбаташон ба 4 баробар бошад».
- «Фарқи ду ададҳо ба 2 баробар, нисбати онҳо ба адади ба 2 чаппа баробар аст. Ин ададҳоро ёбед».
Яъне, дар ин ҷо «нисбат» ба маънии адад кор фармуда шудааст.
Дар китоби VII-и «Ибтидо»-и Евклид назарияи нисбат ва таносуб барои ададҳои бутун баён ёфтааст. Евклид таносуби a:b-c:d -ро навишта аз он ҳосил кардани таносубҳои навро баён кардааст. Хосияти асосии таносубро исбот кардааст: Ҳосили зарби узвҳои канории таносуб ба ҳосили зарби узвҳои мобайнии он баробар аст.
Дар замонҳои гуногун таносубро бо мақсадҳои гуногун истифода кардаанд. Таносуб дар математика, тақсими мерос, меъморӣ, санъат ва щайраҳо ба таври васеъ истифода бурда мешуд ва истифода бурда мешавад.
Мафҳуми давра дар замонҳои пеш аз солшумории мо мавҷуд будааст. Истилоҳҳои радиус ва диаметр низ аз қадим маълум будаанд. Ҳатто дар асрҳои VII-VI-и пеш аз милод Фалеси Милетй кашф кардааст, ки диаметр давра ва доираро ба ду қисмҳои баробар ҷудо мекунад. Радиус лафзи лотинӣ буда, маънояш «нур» аст. Дар асри VI Боэтсий ба ҷойи «радиус» истилоҳи «нимдиаметр»-ро истифода кардааст. Ситсерон (асрҳои II-I-и то милод) гуфтааст, ки «кура аз радиусҳои (нурҳои) баробари аз як нуқта бароянда ташкил мешавад». Лафзи «хорда» юнонй буда, маънояш «тор» аст ва он дар асрҳои XII-XIII аз тарафи олимони аврупоӣ дохил карда шудааст. Ба расандаи давра дар нуқтаи расиш перпендикуляр будани радиуси ба ин нуқта гузаронидашударо Архит Таренский (солҳои 430-365 то милод) медонистааст.
Бо харфи л ишорат кардани нисбати дарозии давра ба диаметрро дар соли 1748 Леонард Эйлер пешниҳод кардааст.
Ба ҳисобкунии қимати л аз замонҳои пеш аз милод бисёриҳо машщул шудаанд, ки аз ҳисобкунии дарозии давра ва масоҳати доира вобаста аст. Мисриҳои қадим барои л қимати 3,1605-ро нишон додаанд. Донишманди чинӣ Чҷан-Хен л-3,162 нишон додааст. Ҳоло дар бисёр ҳисобкуниҳо қимати л -ро ба 3,1416 баробар мегиранд.
Щиёсиддин Ҷамшеди Кошӣ барои л қимати 3,1415926535897932- ро нишон додааст.
Масъалаҳои хатҳои рости параллел аз замонҳои хеле қадими асрҳои гузаштаи пеш аз милод маълум буданд. Аз р=и маъхазҳои мавҷуда ба ин масъалаҳо Фалеси Милетй (асрҳои YII-YI то милод) низ машщул будааст. Дастовардҳои илмии то замони худаш мавҷуд бударо ҷамъбаст карда Евклид (асри IV то милод) рисолаеро иборат аз 11 китоб бо номи «Ибтидо» менависад, ки мащзи асосии он то ҳоло дар китобҳои дарсӣ маъво гирифтаанд. Дар ин рисола оиди хатҳои рости параллел маълумоти мукаммал дода шудааст. Яке аз гуфтори (аксиомаи) дар ин китоб омада: «Аз нуқтаи берун аз хати рост ба ин хати рост параллел карда фақат якто хати рост гузаронидан мумкин аст» буд, ки мо низ онро мутолиа кардем. Дар атрофи ин масъала баҳсҳои тулонӣ давом ёфтанд. Аммо баъди асри V-и милод, бо баъзе сабабҳо, тадқиқоти илмӣ дар Аврупо қатъ гардида, маркази илмӣ ба Шарқ сафар кард. Шарқиён на танҳо илми юнониҳои қадимро нигохдорӣ карданд, балки худашон ба дастовардҳои муҳими илмӣ ноил гардида, маҳзари илмро парратар намуданд. Онҳо оиди хатҳои рости параллел низ пешравиҳо доштанд, ки як қисмашон, бо сабабҳои маълум, то асрҳои VIII-IX милод омада нарасиданд. Аммо дар асрҳои XI- XIII боз ба ҷониби ин масъала р= оварданд, ки намояндагони асосӣ Умари Хайём (асри XI), Насируддини Тусӣ, Қутбиддини Шерозӣ (асри XIII) ва дигарон буданд.
Умари Хайём дар соли 1077 рисолаи «Рисола фӣ шарҳ мо ашкола мин мусодарот китоб-ил Уклидус» (Шарҳи постулатҳои душвори китоби Евклид)-ро менависад. Ин рисола аз се китоб иборат буда, китоби якум назарияи хатҳои рости параллелро дарбар мегирад.
Тараққиёбии саноат, касбу ҳунар, меъморӣ, баҳрнавардӣ ва щайра сабаб шуданд, ки Аврупоиён боз ба илм р= оварданд. Риёзидонҳои онҳо дар донишгоҳҳои Шарқ илм ом=хтанд ва ба чопи рисолаҳои илмии худ низ машщул шуданд. Донишманди фаронсавӣ Рене Декарт (асри XVII) ба ададҳои мусбату манфӣ аз нуқтаи назари дигар баҳо дода, амалҳо бо онҳоро асоснок кард. Вай ин ададҳоро бо нуқтаҳои хати рости координата тасвир намуд ва вобаста ба ин, системаи росткунҷаи координатаҳо ва ҳамвории координатиро ба илм дохил кард, ки ин дигаргунии қатъӣ дар инкишофи минбаъдаи илм буд.











Комментарии (0)